束缚于磁结构中的高能电子具有损失锥速度分布特征。在速度空间中，这种分布在垂直方向上具正梯度（∂f/∂v_⊥>

0），可引发动力学不稳定性及波的激发。在等离子体频率远小于电子回旋频率时（ω_pe/Ω_ce< < 1），此类分布可激发电子回旋脉泽辐射（electron

Cyclotron Maser: ECM）；当ω_pe/Ω_ce>> 1，则可激发Z模脉泽不稳定性，获得增强的Z模扰动。Z模是X模的低频对应分支，可视为垂直或倾斜磁场传播的朗缪尔波。随日心距增加，等离子体特征频率下降很快，使得该模式无法直接离开源区附近而远处传播。研究表明，在某些条件下，Z模扰动可通过波模转换等过程，变为高频电磁模式（O模或X模），成为可观测的射电爆发，这称为Z模脉泽辐射。

太阳射电IV型暴是一种宽频辐射，有时会叠加有斑马纹等精细结构。观测表明，IV型暴应该是由束缚于闭合磁结构中的高能电子所激发的，但具体辐射机制尚不清楚。等离子体相干辐射和非相干的电子回旋同步辐射均曾被用来解释IV型暴。对于连续谱和斑马纹，许多研究人员也认为二者具有不同的辐射机制。也有些研究指出Z模脉泽辐射可同时解释IV型暴连续谱和斑马纹特征，是一种“统一”理论。最近对运动IV型暴的一系列观测研究（Vasanth

et al., 2016, 2019）也在一定程度上支持这种辐射机制。

对于Z模脉泽辐射，以往研究多基于冷等离子体假设，鲜有考虑热效应对Z模不稳定性的影响。在少数考虑背景等离子体温度（T₀）和能量电子能量（v_e）影响的研究中，仅考虑了个别离散的参数值，对应于很不完整的参数研究；此外，对于二者的影响，在几个研究工作还得到了不太一致的结论。其次，以往多分析最大增长率（γ_max）随等离子体特征频率比（ω_pe/Ω_ce）的变化，较少关注其它参数如传播角（θ）和增长波频率（ω）的变化。为了弥补这些缺失，本研究考虑T₀和v_e在给定范围内的连续变化，并考虑该变化对Z模增长有关参数的影响。

为与以往研究比较，本工作仍采用DGH速度分布函数。该函数是一种损失锥类型的速度分布，在垂直速度方向上有个峰值，对应于垂直速度方向上的速度分布函数正梯度，如图1所示。我们使用线性Vlasov动理论波动方程数值求解了Z模不稳定性增长率、增长频率及传播角等参数。结合运动IV型暴最新观测，选取了如下参数范围：0≤T₀≤ 8 MK（~[0, 1] keV），0.15

c ≤ v_e≤ 0.4 c（~[5,

50] keV），10≤ω_pe/Ω_ce≤30。

本工作研究了两种情况，一是固定特征频率比（ω_pe/Ω_ce），二是改变特征频率比，研究该比值对Z模不稳定性的影响。

发现，在固定频率比（ω_pe/Ω_ce=15）时，（1）γ_max随v_e增加总体上呈下降趋势，而随T₀的变化趋势与v_e参数的具体数值有关；（2）随T₀和v_e的连续增加，ω^r_max呈现出明显的阶梯状跳变，在跳变前后则为渐变，分析表明，这主要是由主导谐波次（即Z模增长率最大的谐波次）在特定参数上的变化引起的；（3）相应Z模传播方向总是与磁场方向垂直或基本垂直，且传播角（θ_max）展现出与ω^r_max同步的变化。参见图2。

在变化频率比（10≤ω_pe/Ω_ce≤30）时，主要考察了T₀和v_e对γ_max~ω_pe/Ω_ce曲线峰值和相邻峰谷比（用于衡量曲线平滑度）的影响（见图3和图4），发现：（1）曲线最显著的特征就是准周期的波峰和波谷，相邻峰间差约一Ω_ce，这种Z模的增长特征已被以往研究用来解释观测到的斑马纹结构；（2）随ω_pe/Ω_ce的增加，曲线峰谷比总是减小，并且曲线峰值位置向ω_pe/Ω_ce小的方向移动；（3）曲线峰谷比随T₀增加基本不变；在v_e≤0.3

c时，峰谷比随v_e增加整体呈下降趋势，对应于减弱的斑马纹特征；对于更大的v_e，则峰谷比低于1.2，这对应于不含斑马纹的IV型暴连续谱辐射。

上述参数研究表明，太阳爆发过程中的加热和加速过程会对IV型射电暴和相应斑马纹特征产生重要影响，就导致斑马纹的出现和消失，也会导致相应纹带频率的起伏变化。在将来工作中，应细致考虑这些参数的影响。

该研究结果《Effect of the Temperature of Background Plasma and the Energy of

Energetic Electrons on Z-Mode Excitation》已被ApJ接受发表，全文链接https://arxiv.org/abs/1906.01218。作者感谢国家自然科学基金的支持。

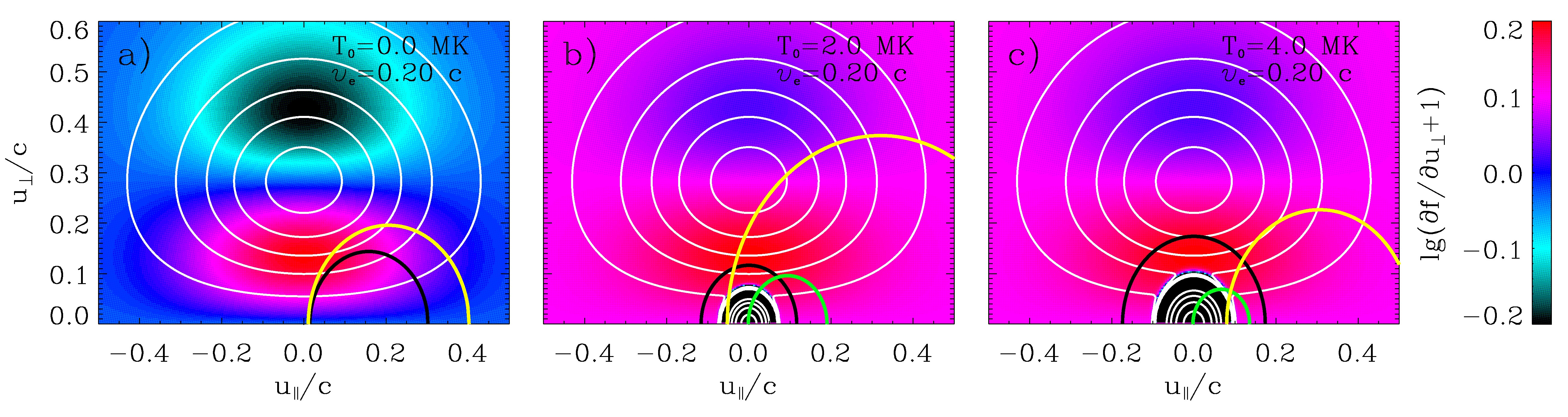
图1：电子速度分布函数f(u_⊥,u_∥)=n_e/n₀f_e+(1–n_e/n₀)f₀示例（白色等值线），，式中n_e/n₀为高能电子所占比例，f_e为DGH速度分布函数，f₀为麦克斯韦速度分布函数。彩图表示相应函数lg(∂f/∂u_⊥+1)在速度空间的分布情况，该函数三个分图依次对应于T₀= 0，2和4 MK，固定v_e为0.2 c。黑（黄、绿）色的曲线代表选择的共振曲线。

图2：从上到下，依次为Z模不稳定性的增长频率（ω^r_max）、角度（θ_max）和相应最大增长率（γ_max）随T₀（左）和v_e（右）的变化曲线。

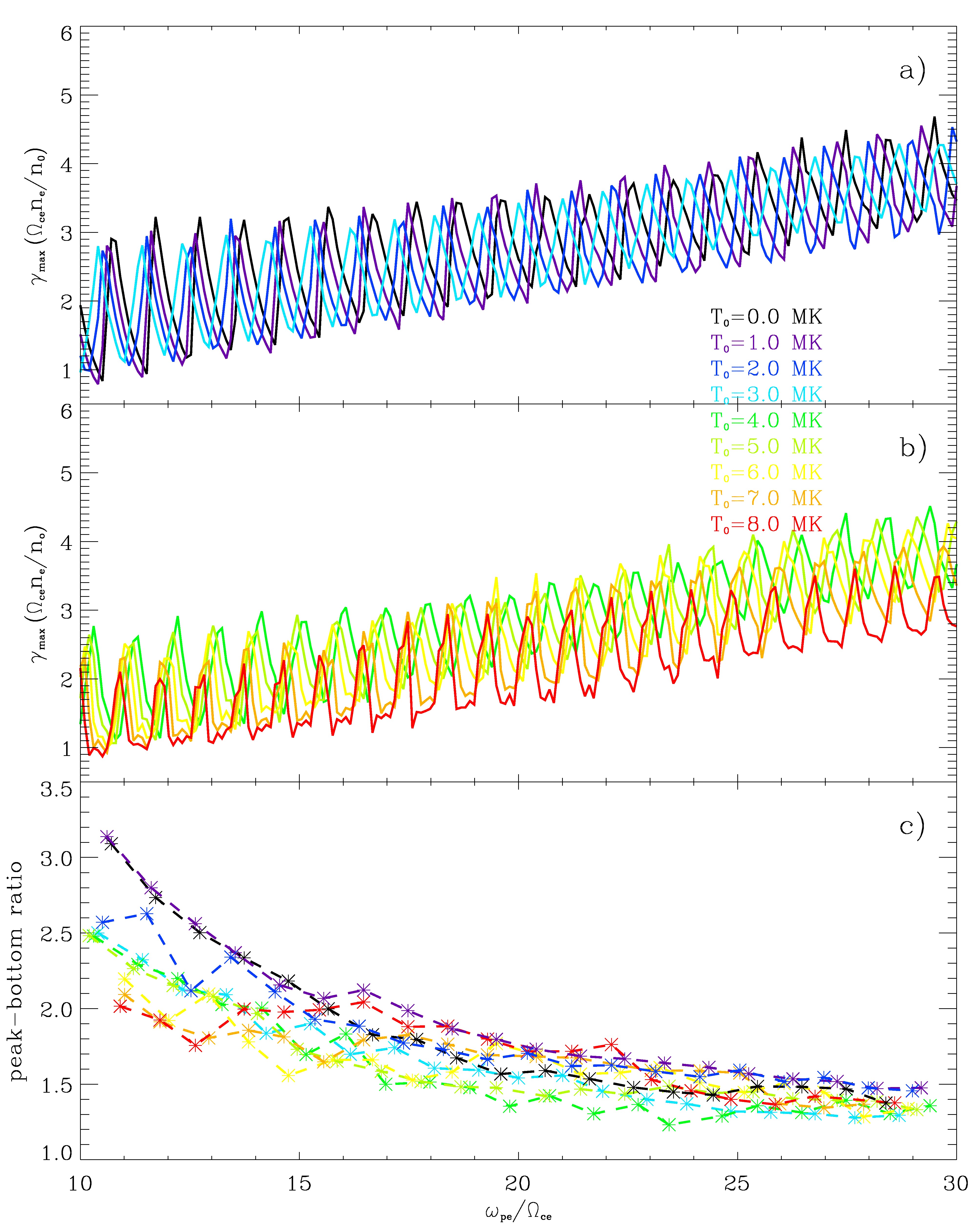
图3：(a–b)γ_max随ω_pe/Ω_ce的变化，各条曲线对应于不同的T₀数值（0 – 8 MK），v_e固定为0.2 c。(c)γ_max~ω_pe/Ω_ce变化曲线的相邻峰值和谷值之比随特征频率比的变化曲线，该比值可用来表示相应曲线的平滑度。

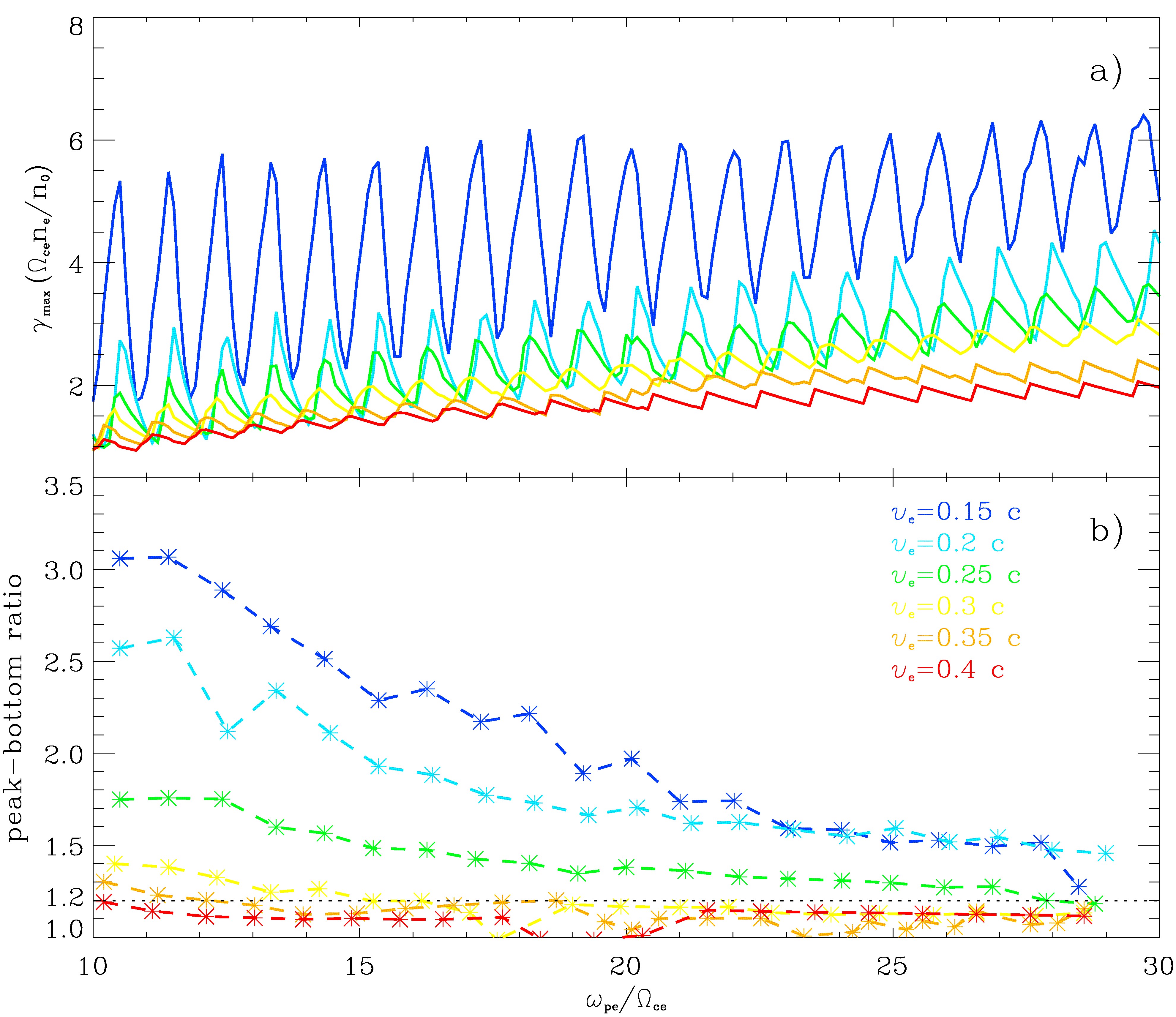
图4：(a)γ_max随ω_pe/Ω_ce的变化，各条曲线对应于不同的v_e数值（0.15 - 0.4 c），T₀固定为2 MK。(b)γ_max~ω_pe/Ω_ce变化曲线的相邻峰值和谷值之比随特征频率比的变化曲线，该比值可用来表示相应曲线的平滑度，黑色虚线表示峰谷比为1.2。